Brownie maths continued...

We don't end it there, Liz and I went on a spree to find out more about our brownie conundrum...

We weren't satisfied with knowing just a couple of good combinations, we wanted to know how one could work out the optimum number of slices for any brownies.

The maths:

If we assume a rectangular pan, and we divide the longest side into 'a' slices, then we need to work out how many slices we need to cut the shorter side into (we'll call this 'b') in order to have an equal number middle and edge slices (we'll call the number of middles 'm' and the number of edges 'e' as we did before).

Now, we know that the number of edge peices is simply the circumference of our pan, so:

e = 2(a+b)-4      (adapted from our square-tin circumference equation)

We also know that the number of middle pieces is found by multiplying the sides, minus the ones that are touching the edges (ie, 2 per side) so:

m = (a-2)(b-2)

Now, we want the same middle as edge, so

             m = e

(a-2)(b-2) = 2(a+b)-4

So, if we solve this to calculate b for a given a:

Liz gets full credit for doing this. I cheated and consulted WolframAlpha, mostly to get the pretty pictures of the steps for solving the above.

The solution Liz (and then Wolfram) came to looked like this:

 And with a little tarting up, I present to you (drumroll please)

The Equation for Equating Brownie Edge and Middle Peices:

Notice, firstly, that there's no solution for having 4 slices on the longest side.

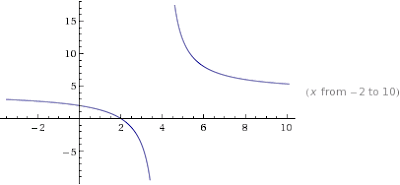
Oh, you want a graph of that? Really? Go on then:

Graph of middle:edge brownie equality for a rectangular tin:

x-axis: Slices on Longer side

y-axis: Slices on Shorter side

In this graph you can clearly see a few of our favourite combinations. 8x6 is on there, as is 12x5.

You can also clearly see that there's no whole-number solution below 4, and no solution at all at 4.

If we consider whole-number (discrete) solutions only, we can build the sequence:

1. 5 x 12
2. 6 x 8
3. 8 x 6
4. 12 x 5

And since 4 is not a solution, we've just defined our complete set of possible solutions. So if you want an equal number of edge to middle brownie slices, you have a choice of 48 or 60 brownies in a 8x6 or 12x5 configuration.

I'll stop maths-geeking out now, I promise...

Brownies...

To quash the allegations, I'm talking about the delicious baked cake-esque treat, not the club for delicious small girls. So there.

A discussion arose yesterday on the benefits of brownies - specifically the difference between "edge bits" and "middle bits".  Now, I'm a middle-bit man. I can't see the appeal of dried, crunchy, crusty edge bits of brownie when the whole point of a brownie is it's squidgy goodness. Alas, I have to concede that I'm in the minority, most people, when fighting for brownie will fight for the edge bits. Indeed, there's special tins to maximise the occurance of edges:

I can already hear the clamour of all you poor, misguided souls looking for a place to buy this small example of cooking geekery. Alas, there exists no 'edgeless' brownie tin (yet).

I am, however, lucky.

My wonderful girlfriend happens to be one of the edge-piece sheep, and so we can get along by my eating the middles bits, and her the outside, right? Surely this is an elegant solution that satisfies both parties? Wrong. We first have to devise a way of cutting up our brownie so that we each get an equal number of brownie pieces.

This leads to a veritable conundrum, how do we cut up our pan?

E = Edge, M=Middle

1x1
E  1 edge, no middle :/

2x2
E E
E E  4 edge, 0 middle

3x3:
E E E
E M E   8 edge, 1 middle (she's still fine with this, apparently)
E E E

4x4:
E E E E
E M M E
E M M E 12 edge, 4 middle (3:1, uncool)
E E E E


...I'm going to skip ahead here...


6x6:
E E E E E E
E M M M M E
E M M M M E
E M M M M E 20 edge, 16 middle (5:4, getting better...)
E M M M M E
E E E E E E


7x7:
E E E E E E E
E M M M M M E
E M M M M M E 24 edge, 25 middle (Ah-ha! we see the tables have turned..)
E M M M M M E
E M M M M M E
E M M M M M E
E E E E E E E


So, the switch happens between 6 and 7 to an edge. Of course, these are square tins. One can work out the ratio easily enough:


where n = length of a side, e = number of edge pieces and m = number of middle peices


e = 4n-4
m = (n-2)^2


And so if we declare that m = e, we can solve the above for n:


(n-2)^2 = 4n-4


<<GCSE MATHS MAGIC>>

n = 4+sqrt(8)   ~= 6.83



Now, I defy any of you to cut a pan exactly into 6.83 brownies a side. In the universal language of 4chan: Pics or GTFO.


Anyway, much more discussion was had before we had a dual revelation:


1: We don't have to have the same number on each side, and
2: Who the hell makes perfectly square baking tins anyway?!


This is game changing, and very quickly, we came to the magic number:


8x6:
E E E E E E E E
E M M M M M M E
E M M M M M M E 24 edge, 24 middle (Win!)
E M M M M M M E
E M M M M M M E
E E E E E E E E




So there you have it. If you find yourself in a situation where the ratio of edge to middle brownies is critical to the continuation of the human race, you're equipped with the tools to work it out. You can thank me later, preferably with baked goods.

EDIT

Miss Firefly_liz informs me that there's another magic ratio: 12x5.

Keep 'em coming! :)

Feral Marmot's Alan

Alan - Zoom-Blur, a photo by Mikebert4 on Flickr.

Just another snap of Alan from Feral Marmot - check out the cheesy zoom-blur.

Excellent morning session it was.

Large Stones and Angular Momentum

Good Morning all,

I apologise for my absence, I've been on holiday in Wales for a time - you'll get more on this later, but first let me tell you about my exploits before heading off to the hilly places.

On my way over to Suffolk to meet Liz and drag her off to Wales I stopped by at Chicksands Bike Park in Bedfordshire to get some riding and shooting done with Alan from Feral Marmot Films. It's always fun to get out to Chicksands with it's selection of marvellous freeride, downhill, cross-country, Dual Slalom and 4X courses.

The day started well (and late, but that was my fault). A couple of warm-up runs down the Dual Slalom and then it was over the back to the last descent of the XC course for some nice sedate shooting before lunch.

Wide-angle of me hitting one of the berms

More Photos can be found on Feral Marmot's Flickr and on their Facebook page (linked above).

Of course, Alan wasn't just behind the lens - I'd brought my camera along and so we got a few shots of Alan strutting his stuff on the same section...

Alan railing the same berm

More can be found on my Flickr


After a rather nice hour or so sedately shooting this little section of trail we decided to head over to the Bike Park proper and get some shooting done on the Dual Slalom and 4X tracks. Alas, the weather had different ideas and it was about this time that it started really chucking it down with rain.

It persisted it down.

We packed up the kit and in the absence of waterproofing gear, we high-tailed it back to the cars to dump it all. Unfortunately, it didn't stop raining for the next 2 hours. We made one forray back into the park during a light spell to see if anything was ridable given the shear volume of water that had just been dumped on it. Alas, whilst the DS course was navigable, it wasn't really conducive to any great speed or airborne shenagians. We had to abandon our day early, I headed onto Suffolk and Alan headed back to Peterborough and Feral Marmot HQ.

Still, it was a great, if slightly wet, day's shooting.

..that you believed in superstition

Blog time!

Why?

Good question, I'll tell you why.

I have 3 hours to kill at London City is why. I could've gone home, sure, I could have adopted a penguin. My point is, I didn't. I decided to kill time here (kill time, that is - not the penguin. Penguins are awesome).

Today and the next two days work a little like this:

1. Get up Way Too Early
2. Operate some Frankfurt/Zurich sectors
3. Wait
4 PROFIT! Position out to Frankfurt to nightstop.

Easy enough? Yeah, you'd think that, because it doesn't look to bad. Actually, you're right, it's a pretty easy tour. All I have to do is keep myself from spending monies on hotel food - or 'going out and eating' food. This shaln't be difficult because at the moment I have no money. I shall be a model of fiscal responsibility thanks to my rather appalling fiscal situation. I feel somewhat like the UK economy, in this respect.

Today's big gotcha was a problem with the aircraft I took to Zurich this morning - the autobrake had failed at some point during the night and so we were presented with the MEL sat on the centre console. If you learn one thing about airline flying, it's that opening up a flight deck to see the MEL open at a relevant page on the centre console is a big sign that your day just got more complicated in some way.

MEL - Minimum Equipment List.
A book that, counter-intuitively, lists everything that you can go without. It lists systems, items, failures etc that are acceptable to dispatch with and the special procedures you need to execute/complete to make the flight safe.
As a rule, if something is missing or broken and it's not in the MEL, you cannot go (it's not quite this simple - there's another list called the CDL and also the engineers can 'defer' some defects and you can still go). All sorts of things are in the MEL - for example you can fly without a winglet (vertical bit on the end of the wing) - so long as there's no passengers and you're flying back to a maintenance base, and several other things.

Stuff I've had in the past included having a engine bleed out (only half as much air conditioning) - meaning we couldn't fly above FL310 (31,000ft), and the Right-hand side MFD (Multi-Function Display - go go pointless acronyms!) - which is basically my screen with a map on it - meaning that any low-visability stuff had to be flown from the captain's side.

Today it was Autobrake. Dead easy. Brake Manually. I kid you not.

Other than that, an uneventful day. I shall now go back to aimlessly wandering around the internet in search of funnies.

tl;dr: Mike bored.

Aerobatics

Blade Extra 300LP, a photo by Mikebert4 on Flickr.

One day, I shall do this.

That is all.